Cho số phức z thỏa mãn z-i =5 ✅ [Update]
Kinh Nghiệm Hướng dẫn Cho số phức z thỏa mãn z-i =5 Mới Nhất
Hoàng Gia Trọng Phúc đang tìm kiếm từ khóa Cho số phức z thỏa mãn z-i =5 được Cập Nhật vào lúc : 2022-11-23 04:16:06 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
DẠNG TOÁN 42 TÌM SỐ PHỨC THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC – phát triển theo đề tham khảo Toán 2022
Theo đề tham khảo Toán 2022 của Bộ GD&ĐT
ĐỀ BÀI:
Có bao nhiêu số phức Z thoả mãn ((1 – 3i)z) là số thuần ảo và (z^2=(1+i)|z|-2(1-i))?
A.(4).
B. (2).
C. (3).
D. (0).
LỜI GIẢI CHI TIẾT
Gọi (z = a + bi) với (a,b in mathbbR).
+ Ta có ((1 – 3i)z = left( 1 – 3i right)left( a + bi right) = left( a + 3b right) + left( b – 3rma right)i).
Do đó ((1 – 3i)z) là số thuần ảo ( Leftrightarrow a + 3b = 0 Leftrightarrow a = – 3bleft( 1 right))
+ Ta có (z^2=(1+i)|z|-2(1-i)) ( Leftrightarrow z^2=|z|+i|z|-2+2i => z^2=|z|-2+(|z|+2)i )
Lấy môđun hai vế, ta được (left| z^2 right| = sqrt left( left right)^2 + left( z right right)^2 )
Do (|z|^2=|z^2|) nên khi để (t=|z|^3) ta được (t^2 = sqrt left( t – 2 right)^2 + left( t + 2 right)^2 )
( Leftrightarrow t^4 = t^2 – 4t + 4 + t^2 + 4t + 4 Leftrightarrow t^4 – 2t^2 – 8 = 0 Leftrightarrow left[ beginarraylt^2 = – 2\t^2 = 4endarray right.)
( Rightarrow left| z right| = 2 Leftrightarrow a^2 + b^2 = 4left( 2 right)).
Từ,ta có (left{ beginarrayla = – 3b\a^2 + b^2 = 4endarray right. Leftrightarrow left[ beginarraylleft{ beginarrayla = – frac3sqrt 10 5\b = fracsqrt 10 5endarray right.\left{ beginarrayla = frac3sqrt 10 5\b = frac – sqrt 10 5endarray right.endarray right. Leftrightarrow left[ beginarraylz = – frac3sqrt 10 5 + fracsqrt 10 5.i\z = frac3sqrt 10 5 – fracsqrt 10 5.iendarray right.).
Thử lại, với (z = – frac3sqrt 10 5 + fracsqrt 10 5.i) thì (z^2 = frac25left( 8 – 6i right)) và (left| z right| = 2).
Khi đó (left( 1 + i right)left| z right| – 2left( 1 – i right) = 2left( 1 + i right) – 2left( 1 – i right) = 4i) không thỏa mãn.
Với (z = frac3sqrt 10 5 – fracsqrt 10 5.i) thì (z^2 = frac25left( 8 – 6i right)) và (left| z right| = 2).
Khi đó (left( 1 + i right)left| z right| – 2left( 1 – i right) = 2left( 1 + i right) – 2left( 1 – i right) = 4i) không thỏa mãn.
Vậy không còn số phức nào thỏa mãn bài toán.
Thu gọn $z = left( sqrt 2 + 3i right)^2$ ta được:
Trong những kết luận sau, kết luận nào sai:
Tìm số phức phối hợp của số phức $z = 3 + 2i$.
Phương trình bậc hai nào sau đây có nghiệm là (1 + 2i?)
Phương trình: $8z^2 - 4z + 1 = 0$ có nghiệm là:
Cho số phức z thỏa mãn (|z|=5) và (|z+3|=|z+3-10i|). Tìm số phức (w=z-4+3i.)
A.
B.
C.
D.
Mã thắc mắc: 152316
Loại bài: Bài tập
Chủ đề :
Môn học: Toán Học
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, nhấn vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho số phức z thỏa mãn (left| z-2i right|le left| z-4i right|) và (left| z-3-3i right|=1). Trong tập những số phức, cho phương trình (z^2-6z+m=0), (min mathbbR) (left( 1 right)). Gọi (m_0) là một giá trị của (m) để phương trình (left( 1 right)) có hai nghiệm phân biệt (z_1), (z_2) thỏa mãn (z_1.overlinez_1=z_2.overlinez_2). Hỏi trong khoảng chừng (left( 0;,20 right)) có bao nhiêu giá trị (m_0in mathbbN)? Gọi số phức (z=a+bi), (left( a,b,in mathbbR right)) thỏa mãn (left| z-1 right|=1) và (left( 1+i right)left( overlinez-1 right)) có phần thực bằng (1) đồng thời (z) không là số thực. Khi đó (a.b) bằng : Cho số phức z thoả mãn(frac1+iz) là số thực và (left| z-2 right|=m) với (min mathbbR). Gọi (m_0) là một giá trị của m để có đúng một số trong những phức thoả mãn bài toán. Khi đó: Trong tập hợp những số phức, gọi (z_1), (z_2) là nghiệm của phương trình (z^2-z+frac20224=0), với (z_2) có thành phần ảo dương. Cho số phức z thoả mãn (left| z-z_1 right|=1). Giá trị nhỏ nhất của (P=left| z-z_2 right|) là Gọi S là tập hợp những số thực m sao cho với mỗi (min S) có đúng một số trong những phức thỏa mãn (left| z-m right|=6) và (fraczz-4) là số thuần ảo. Tính tổng của những phần tử của tập S Cho những số phức z thỏa mãn (left| z-i right|=5). Biết rằng tập hợp điểm màn biểu diễn số phức (w=iz+1-i) là đường tròn. Tính bán kính của đường tròn đó. Cho số phức thỏa (left| z right|=3). Biết rằng tập hợp số phức (w=overlinez+i) là một đường tròn. Tìm tâm của đường tròn đó. Cho số phức (z=a+bi) (left( a,bin mathbbR right)) thỏa mãn (z+2+i-left| z right|left( 1+i right)=0) và (left| z right|>1). Tính (P=a+b). Đường nào dưới đây là tập hợp những điểm màn biểu diễn số phức z trong mặt phẳng phức thỏa mãn điều kiện (left| z-i right|=left| z+i right|)? Có bao nhiêu số phức (z) thỏa mãn (left| z right|=left| z+barz right|=1)? Tập hợp những điểm màn biểu diễn số phức (z) thỏa mãn (2left| z-1 right|=left| z+barz+2 right|) trên mặt phẳng tọa độ là một Tìm giá trị lớn số 1 của (P=left| z^2-z right|+left| z^2+z+1 right|) với z là số phức thỏa mãn (left| z right|=1). Cho số phức z và w thỏa mãn (z+w=3+4i) và (left| z-w right|=9). Tìm giá trị lớn số 1 của biểu thức (T=left| z right|+left| w right|). Trong mặt phẳng phức, gọi A, B, C, D lần lượt là những điểm màn biểu diễn số phức (z_1=-1+i), (z_2=1+2i), (z_3=2-i), (z_4=-3i). Gọi S là diện tích s quy hoạnh tứ giác (ABCD). Tính S Cho số phức z thoả mãn (left| z-3-4i right|=sqrt5). Gọi M và m lần lượt là giá trị lớn số 1 và giá trị nhỏ nhất của biểu thức (P= z+2 right^2-^2). Tính môđun của số phức (w=M+mi). Cho số phức z, biết rằng những điểm màn biểu diễn hình học của những số phức z; iz và (z+iz) tạo thành một tam giác có diện tích s quy hoạnh bằng 18. Mô đun của số phức z bằng Cho số phức z thỏa mãn (left| z right|=2). Biết rằng tập hợp những điểm màn biểu diễn số phức (w=3-2i+left( 2-i right)z) là một đường tròn. Bán kính R của đường tròn đó bằng ? Cho số phức z thỏa mãn (4left| z+i right|+3left| z-i right|=10). Giá trị nhỏ nhất của (left| z right|) bằng: Trong mặt phẳng tọa độ (Oxy), gọi M, N, P lần lượt là những điểm màn biểu diễn những số phức (z_1=1+i), (z_2=8+i), (z_3=1-3i). Khẳng định nào sau đây đúng? Có bao nhiêu số phức z thỏa mãn (left| fracz-1z-i right|=left| fracz-3iz+i right|=1)? Số phức (z=a+bi) ( với a, b là số nguyên) thỏa mãn (left( 1-3i right)z) là số thực và (left| overlinez-2+5i right|=1). Khi đó a+b là Cho hai số phức (z_1), (z_2) thỏa mãn (left| z_1+5 right|=5,,,left| z_2+1-3i right|=left| z_2-3-6i right|). Giá trị nhỏ nhất của (left| z_1-z_2 right|) là Cho số phức (w=x+yi), (left( x,,,yin mathbbR right)) thỏa mãn điều kiện (left| w^2+4 right|=2left| w right|). Đặt (P=8left( x^2-y^2 right)+12). Khẳng định nào dưới đây đúng? Cho số phức (z=a+bi) (left( a,text bin mathbbR right)) thỏa mãn (z+1+3i-left| z right|i=0). Tính (S=a+3b).
đã hỏi trong Lớp 12 Toán học
· 10:04 29/08/2022
Cho những số phức z thỏa mãn |z-i|=5. Biết rằng tập hợp điểm màn biểu diễn số phức w = iz+1-i là đường tròn. Tính bán kính của đường tròn đó.
A. r = 20.
B. r = 5.
C. r = 22.
D. r = 4.
Câu hỏi hot cùng chủ đề
Cách chuyển từ sin sang cos ạ ?
Trả lời (32) Xem đáp án »
Cho hàm số y=ax3+bx2+cx+d có đồ thị như hình vẽ. Tìm mệnh đề đúng
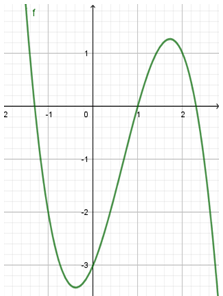
A. a<0, b>0, c>0, d<0
B. a<0, b<0, c>0, d<0
C. a>0, b>0, c>0, d<0
D. a<0, b>0, c<0, d<0

Post a Comment